


Das nach Blaise Pascal benannte Pascalsche Dreieck, bzw. eine grafische Darstellung der Binomialkoeffizienten existierte bereits
seit dem 10. Jahrhundert. Zunächst in Indien von Halayudha und in Persien von Omar Chayyam bekannt gemacht, wurde es um 1261 in China
von Yang Hui veröffentlicht.
Seit 1527 gibt es diese Darstellung in Europa, zunächst veröffentlicht von Peter Apian. 1655 schließlich
verwendete Pascal die dreieckförmige Darstellung der Binomialkoeffizienten, um u.a. Probleme der Wahrscheinlichkeitstheorie zu lösen.
Seit 1708 wird das Dreieck nach ihm benannt (zumindest bei uns; im Iran heißt es Chayyam-Dreieck, in Italien Tartaglia-Dreieck und in
China Yang-Hui-Dreieck).
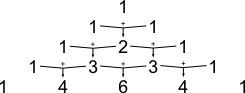
Das Bildungsgesetz des Dreiecks ist denkbar einfach. Zunächst gibt es in der ersten Zeile nur einen Eintrag; die 1. In der zweiten Zeile gibt es zwei Einträge; 1 und 1. In jeder neuen Zeile beginnen die Einträge mit 1 und enden auch mit 1. Jeder weitere Eintrag ergibt sich aus der Summe der beiden über ihm stehenden Einträge.
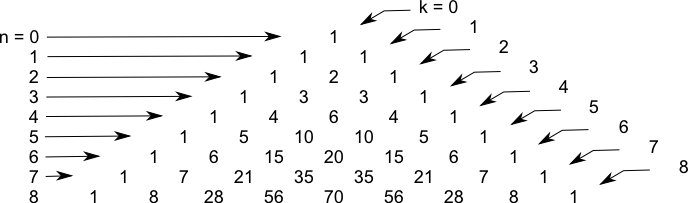
Jede Zeile und jeder Eintrag in der Zeile wird durchnummeriert, beginnend bei 0. Die erste Zeile ist also n = 0, für den zweiten Eintrag in der
dritten Zeile gilt n = 2 und k = 1. So lassen sich die Zahlen in dem Dreieck zunächst als Koeffizienten eines mit n potenzierten Binoms auffassen.
Dieses Binom sieht folgendermaßen aus:
$$
\left( a + b \right)^n
$$
Einige Beispiele:
\begin{align}
n = 0&: \left( a + b \right)^0 = \color{blue} {1} \\
n = 1&: \left( a + b \right)^1 = \color{blue} {1} \cdot a + \color{blue} {1} \cdot b \\
n = 2&: \left( a + b \right)^2 = \color{blue} {1} \cdot a^2 + \color{blue} {2} \cdot ab + \color{blue} {1} \cdot b^2 \\
n = 3&: \left( a + b \right)^3 = \color{blue} {1} \cdot a^3 + \color{blue} {3} \cdot a^2b + \color{blue} {3} \cdot ab^2 + \color{blue} {1} \cdot b^3 \\
\ldots \\
n = 6&: \left( a + b \right)^6 = \color{blue} {1} \cdot a^6 + \color{blue} {6} \cdot a^5 b + \color{blue} {15} \cdot a^4 b^2 + \color{blue} {20} \cdot a^3 b^3 + \color{blue} {15} \cdot a^2 b^4 + \color{blue} {6} \cdot ab^5 + \color{blue} {1} \cdot b^6
\end{align}
Für n = 2 ist das die bekannte erste binomische Formel. Allgemein kann der binomische Lehrsatz formuliert werden:
$$
\left( a + b \right)^n = \sum_{k = 0}^n \binom {n}{k} \cdot a^{n-k} \cdot b^k
$$
Der Ausdruck $\binom {n}{k}$ ergibt den jeweiligen Koeffizienten, z.B. $\binom {2}{1} = 2$ oder $\binom {4}{2} = 6$. Für $n = 4$ lautet der Lehrsatz ausführlich: \begin{align} \left( a + b \right)^4 &= \binom {4}{0} \cdot a^{4-0} \cdot b^0 + \binom {4}{1} \cdot a^{4-1} \cdot b^1 + \binom {4}{2} \cdot a^{4-2} \cdot b^2 + \binom {4}{3} \cdot a^{4-3} \cdot b^3 + \binom {4}{4} \cdot a^{4-4} \cdot b^4 \\ \left( a + b \right)^4 &= 1 \cdot a^4 + 4 \cdot a^3 b + 6 \cdot a^2 b^2 + 4 \cdot a b^3 + 1 \cdot b^4 \end{align}
Eine andere Lesart des Ausdrucks $\binom {n}{k}$ lautet $n$ über $k$ oder aber $k$ aus $n$. Die zweite Sprechweise kennt man wahrscheinlich aus dem Lotto:
6 aus 49. Das bedeutet, dass der siebte Eintrag in der 50. Zeile gesucht ist (k = 6, n = 49). Die Zahl, die dort steht, ist die 13983816. Das wiederum
bedeutet, dass es 13983816 verschiedene Möglichkeiten gibt, sechs Zahlen aus 49 mögliche Zahlen auszuwählen.
Typischerweise werden so Anordnungsprobleme aus der Kombinatorik gelöst. Wieviele Möglichkeiten gibt es, zwei Objekte auf sieben verfügbaren Plätzen
anzuordnen? Die Antwort ist: $\binom {7}{2} = 21$
Eine wichtige Randbedingung ist hierbei, dass die $k$ Objekte nicht voneinander zu unterscheiden sind. Die Reihenfolge der Objekte ist nicht relevant. Es
ist egal, ob Objekt 1 auf Platz 1 ist und Objekt 2 auf Platz 2 oder umgekehrt. Die Plätze 1 und 2 sind von beiden Objekten besetzt.
Die Frage, wieviele Möglichkeiten es gibt, dass drei Läufer ins Ziel kommen, kann so nicht beantwortet werden, da hier die Reihenfolge wichtig ist.
Eine weitere Eigenschaft ist in den Hauptdiagonalen des Dreiecks versteckt. In der 0.Diagonale (k = 0) befindet sich nur die 1 (Punkt; nullte Dimension). In der 1.Diagonalen (k = 1) befinden sich die natürlichen Zahlen (Linie; erste Dimension), in der 2.Diagonalen die Dreieckszahlen (Fläche; zweite Dimension) und in der 3.Diagonalen die Tetraederzahlen (Raum; dritte Dimension).
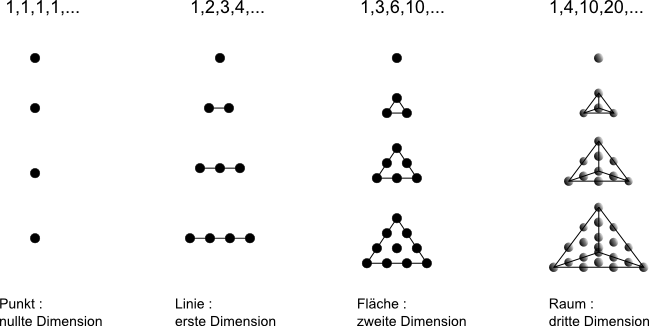
Über die Bedeutung der weiteren Hauptdiagonalen kann nur spekuliert werden...
In den sogenannten Nebendiagonalen sind die Zahlen der Fibonacci-Reihe enthalten. Die Zahlen der Fibonacci-Reihe werden durch die Summe der beiden Vorgängerzahlen gebildet, z.B. 1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8; ...

Ein weiterer Inhalt des Pascalschen Dreiecks ist in den Waagerechten versteckt. Dort sind jeweils die Ziffern für die $n$-te Potenz von 11, also $11^n$.
\begin{align}
n = 0 &: 11^0 = 1 \\
n = 1 &: 11^1 = 11 \\
n = 2 &: 11^2 = 121 \\
n = 3 &: 11^3 = 1331 \\
\ldots
\end{align}
Ab $11^5 = 161051$ muss man allerdings auf den Stellwert der Zahl achten, Ab hier gilt beispielsweise, dass die Zahl eine 1 auf der Einerstelle, eine 5
auf der Zehnerstelle, eine 10 auf der Hunderterstelle (0 auf Hunderter- und 1 auf Tausenderstelle), eine 10 auf der Tausenderstelle (0 auf Tausender- und 1
auf Zehntausenderstelle), sowie eine 5 auf der Zahntausenderstelle (insgesamt 1 + 5 = 6 auf der Zehntausenderstelle) und eine 1 auf der Hunderttausenderstelle
aufweist.
Für den Ausdruck $11^8$ folgt: \begin{align} 1 \cdot 1 &= \qquad \quad \;\;\, 1 \\ 8 \cdot 10 &= \;\;\,\,\,\,\;\;\,\,\,\;\;\;\,80 \\ 28 \cdot 100 &= \;\;\,\,\,\,\;\,\;\,\,2800 \\ 56 \cdot 1000 &= \;\;\,\,\,\,\,\;\,56000 \\ 70 \cdot 10000 &= \;\;\,\,\,\,\,700000 \\ 56 \cdot 100000 &= \;\;\,\,5600000 \\ 28 \cdot 1000000 &= \;\,28000000 \\ 8 \cdot 10000000 &= \;\,80000000 \\ 1 \cdot 100000000 &= 100000000 \\ & \text{_____________} \\ &= 214358881 \end{align}
Die Summe der Zahlen in den Waagerechten entsprechen jeweils der Zweierpotenz $2^n$: \begin{align} 2^0 &= 1 \\ 2^1 &= 1 + 1 = 2 \\ 2^2 &= 1 + 2 + 1 = 4 \\ 2^3 &= 1 + 3 + 3 + 1 = 8 \\ \ldots \end{align}
© mondbrand MMXIX